本网讯（通讯员 郭志军）为切实推进课程建设高质量发展，提升我院青年教师教育教学水平。2025年10月22日下午第六节课，理学院青年教师刘雨晴老师就《高等数学》上册中“两个重要的极限”这一主题开展示范教学。学校督导团领导蒋练军和理学院舒谷生书记、代安定副院长及理学院二位教学督导和数学与计算科学系主任与公共数学教研室主任共计12位老师到场参加听课、评课。示范课整体很成功，示范效果良好。

学校督导团领导与理学院书记及理学院老师课堂听课。

示范课前理学院督导组组织青年老师及经验丰富的老师对刘雨晴及两位新进老师以教研活动的形式经过多轮磨课评课，共同探讨教学过程的设计与教学方法的应用。对青年老师的快速成长起了较大作用。

理学院督导组及其他老师对雨晴老师磨课。

本次示范课中，刘雨晴老师结合教学内容精心设计教学环节，不仅展示了青年老师教学风采也为观摩学习的老师上了一堂成功的示范课，下面从以下三个维度学习她的授课。

一、立德树人：于严谨推理中涵养科学精神，于数学思想中渗透哲学智慧

刘雨晴老师在教学过程中，超越了单纯的知识传授，深刻体现了“立德树人”的根本任务。

首先，在证明极限时，刘老师采用数形结合方法，通过图形将抽象的极限关系可视化，让学生直观感受到数学逻辑，在潜移默化中培养学生尊重科学、追求真理的理性精神。

其次，她在讲解中融入了“以直化曲、化繁为简”的哲理，是对学生世界观和方法论的极好塑造。“以直化曲”体现了辩证法中量变与质变、近似与精确的关系；“化繁为简”则是处理复杂问题的普适性哲学思维。

最后，刘老师通过数学语言，让学生体会到，面对复杂问题，可以通过转化与化归找到突破口，这不仅是数学能力，更是一种宝贵的人生智慧。刘老师通过其精心的设计，将求真务实的科学态度、探索创新的思维品质和辩证唯物的哲学思考自然融入课堂，实现了知识传授与价值引领的有机统一。

刘雨晴老师融入思政教学的PPT。

二、教学方法：聚焦直观与逻辑，注重思维建构与迁移应用

刘雨晴老师始终围绕学生的认知规律展开教学，展现了其先进的教学理念和出色的教学设计能力。

第一，引入环节精准高效。从“两个函数图线在原点附近基本重合”切入，瞬间抓住了核心内容的直观表象，为学生搭建了从感性认知通向理性理解的桥梁，激发了学生的好奇心和探究欲。

第二，证明过程凸显建构性。摒弃枯燥的纯符号推导，选择“单位圆”这一几何模型，将抽象的极限问题转化为直观的图形关系（面积比较），极大地降低了学生的认知负荷。这种“数形结合”不仅是方法的运用，更是帮助学生自主“建构”起对

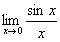极限为何为1的深刻理解，体现了“以学生为中心”的教学思想。

第三，例题设计层次分明，思想渗透到位。刘老师通过精选例题，反复锤炼“如何利用重要极限”这一核心技能，并将“换元”等数学思想作为解题的“钥匙”进行点拨。这使学生不仅掌握了“怎么做”，更明白了“为什么这么做”，实现了从知识到能力，再到思维素养的迁移与升华，有效培养了学生分析问题和解决问题的能力。

刘雨晴老师通过数形结合证明重要极限。

三、教学基本功：结构严谨清晰，表达精准流畅，展现扎实素养

刘雨晴教师展现较为扎实的教学基本功，这是其课堂成功的基础保障。在语言表达方面，她教学语言清晰，表达准确，能够用精炼且专业的数学语言阐述概念、推理证明，确保了信息传递的有效性，让学生能够清晰、无歧义地接收知识，这对于数学这门高度精确的学科至关重要。在教学结构方面，整堂课结构完整，逻辑脉络一气呵成。从贴合核心的直观引入，到严谨而直观的证明环节，再到层层递进的例题应用与思想总结，各环节之间衔接自然流畅，没有出现逻辑断层。这种清晰的结构感，有助于学生在脑海中形成系统化的知识框架，而非零散的知识点。此外，她能将“数形结合”、“化归思想”等较高层面的数学思想不着痕迹地融入教学细节，也反映出其本人对高等数学内容有着深刻的理解和把握。作为一名年轻教师，能具备如此成熟的教学架构能力和清晰的语言表达能力，实属难能可贵，为其未来的专业发展奠定了坚实的基础。

学校督导团副团长蒋练军点评刘雨晴老师授课。

在追求教学卓越的道路上，我们所有老师不仅需要精研教学内容，更需具备“设计思维”与“育人视野”。在教学中强化“方法论”的提炼，引导学生构建清晰的方法论体系更为关键，有意识地带领学生“跳出题海”，对各类解题思路进行系统性的归纳与对比，帮助学生从“会解一道题”升华为“掌握一类方法”，构建起可迁移的认知框架。同时我们应勇于打破数学与现实的壁垒，高等数学不应是悬浮于空的符号游戏，其生命力源于解决实际问题的巨大能量。我们应积极挖掘与教学内容相关的现实案例，无论是工程中的振动分析，还是经济学中的边际模型，用生动的实例揭示抽象公式背后的实用价值。这不仅能点燃学生的学习热情，更能深刻践行“学以致用”的育人目标。（一审：李量夫  二审：金芳  三审：陈暑波）